Original article:http://www.math.stonybrook.edu/~tony/tides/index.html


Halls Harbour, Nova Scotia; och Halls Harbour, sex timmar senare.
från Greenberg , s.128A
* Allmänna saker om tidvatten och tidvattenförutsägelse (denna sida).
* Prover av dagens tidvattenförutsägelser från National Ocean Service och från WWW Tide and Current Predictor .
* Om vattennivåer, tidvatten och strömmar (inkluderar viss historia av tidvattenförutsägelse) från NOAA / NOS-webbplatsen.
* Tide Spectra och Tide Sounds : Det förutsagda tidvattenrekordet för olika hamnar tolkas som musikaliska partitur.
* Tides of the Tides: 3000 timmar från Ancona och Venedig , arrangerad för träblåsare, marimba av Levy Lorenzo.
* Mer detaljerad information om harmonisk tidvattenanalys.
* En trevlig kalkyl med kalkylatorövning: Tidningen av tidvatten.
* Referenser .
OBS: En del av denna information visas i en kolumn i tre delar som jag skrev i april-juni 2001 för “What’s New in Mathematics” på American Mathematical Society webbsida. Del III i kolumnen har en härlig JAVA-animering av en tidvattenprognos på grund av Bill Casselman.
Tidvatten och historia: Tidvattenförutsägelserna för D-Day av Bruce Parker, i Physics Today .
Tidvattenförutsägelse. Människor som går in eller ut ur en hamn eller ankar nära en strand måste veta i förväg om tidvattnets beteende. Tidvattnet orsakas av solens och månens dragning i haven och jordens rotation, men dess exakta mönster på en viss plats på kusten beror mycket starkt på kustens form och på profilens havsbotten i närheten. Så även om de krafter som rör tidvattnet är helt förstådda, är tidvattnet på någon plats i princip omöjligt att beräkna teoretiskt. Vad vi kan göra är att registrera tidvattnets höjd på den platsen under en viss tidsperiod och använda dessa mätningar för att förutsäga tidvatten i framtiden. Här är en typisk tidvattenrekord: den här grafen visar vattnets höjd över fjorton dagar.
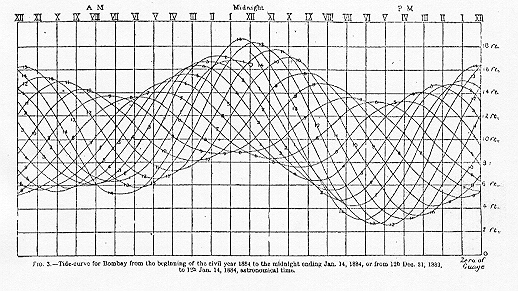
Denna figur visar tidvattenrekordet i Bombay i två veckor (1-14 januari 1884). Tidvattnet registrerades på ett cylindriskt ark som vände var 24: e timme. Varje dagskurva är märkt med sitt datum. Några uppenbara funktioner: det finns vanligtvis två tidvatten och två lågvatten varje dag; tidvattnet kommer cirka 50 minuter senare varje dag; under tvåveckorsperioden finns det stora variationer i det dagliga mönstret för höjder och nedgångar; det finns vanligtvis en höjdskillnad mellan två på varandra följande högvatten (den dagliga ojämlikheten ). [Från GH Darwins artikel om Encyclopaedia Britannica, nu tillgänglig online . Observera att i den här grafen ökar tiden åt vänster .] Större bild .
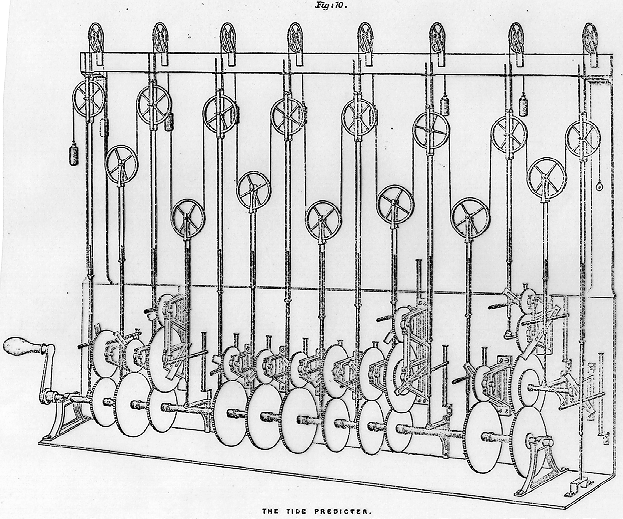
Tide Predicter ( Kelvin , mittemot s. 304).
Tony Phillips
Math Dept SUNY Stony Brook
tony at math.stonybrook.edu
20 maj 1999
länkar uppdaterade 17 mars 2013
Nytt musikmaterial tillagt 23 maj 3015
5 oktober 2015
Teckensnitt justerat 28 januari 2020
Länkar uppdaterat 20 juli 2020
