H. Brönnimann, O. Devillers, S. Lazard, and F. Sottile
original article:https://www.math.tamu.edu/~sottile/research/stories/4triangles/index.html
Vi överväger följande enkla geometriska fråga: Vad är det maximala antalet linjer som tangenterar fyra trianglar? (Det vill säga vi räknar de linjer som möter en kant från varje triangel.) För enkelhetens skull antar vi att trianglarna är i en lämplig allmän position genom att den algebraiska avslappningen där vi byter ut kanter med stödlinjer har endast ändligt många lösningar . (I själva verket 162 distinkta komplexa lösningar.)
Vi ber om det maximalt möjliga antalet, eftersom minimivärdet är noll: Om de fyra trianglarna är tillräckligt långt ifrån varandra, säg i fyra hörn av ett mycket stort rum, kommer det inte att finnas några sådana vanliga tvärgående.
För närvarande är det bästa svaret på denna fråga att det maximala antalet är mellan 62 och 162, med en övre gräns på 156 om trianglarna är ojämna. Den övre gränsen är nästan säkert inte den bästa möjliga, och vi tvivlar också på att den nedre gränsen är optimal. Denna nedre gräns beror på en konstruktion som vi beskriver på den här sidan (länkad till bilden nedan till höger). Denna konstruktion innefattar störande fyra linjesegment med två gemensamma tvärgående, och var och en av de resulterande trianglarna har en extremt liten vinkel – de är ganska tunna. Vår bästa konstruktion med fyra feta trianglar har 40 vanliga tvärgående. En beskrivning av datasökningen som vi använde för att hitta detta exempel är länkad till bilden till vänster nedan, samt animationer.
Denna WWW-sida åtföljer vår artikel om detta ämne, om antalet linjetangenter till fyra trianglar i tredimensionellt utrymme .
Bilderna är länkade till ytterligare diskussion
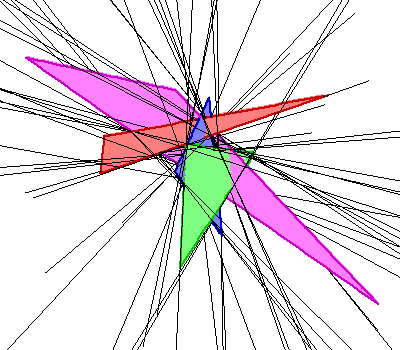 |
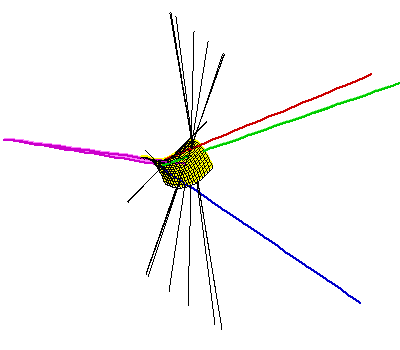 |
|
| Animationer: 841 kB 2100 kB 4198 kB . | Animationer: 86 kB 215 kB . 526 kB . |
Baserat på arbete som stöds av National Science Foundation under CAREER Grant DMS-0134860.
