original article:https://www.evanmiller.org/how-not-to-sort-by-average-rating.html
По Эван Миллер
6 февраля 2009 г. ( Изменения )
ПРОБЛЕМА : вы веб-программист. У вас есть пользователи. Ваши пользователи оценивают материалы на вашем сайте. Вы хотите поместить материалы с самым высоким рейтингом вверху, а с самым низким – внизу. Вам нужна какая-то «оценка» для сортировки.
НЕПРАВИЛЬНОЕ РЕШЕНИЕ №1 : Оценка = (Положительные оценки) – (Отрицательные оценки)
Почему это неправильно : предположим, что один элемент имеет 600 положительных оценок и 400 отрицательных оценок: 60% положительных. Предположим, что элемент 2 имеет 5 500 положительных оценок и 4 500 отрицательных оценок: 55% положительных. Этот алгоритм ставит второй пункт (оценка = 1000, но только 55% положительных результатов) выше первого пункта (оценка = 200 и 60% положительных результатов). НЕПРАВИЛЬНО.
Сайты, которые совершают эту ошибку : Городской словарь

НЕПРАВИЛЬНОЕ РЕШЕНИЕ № 2 : Оценка = Средняя оценка = (Положительные оценки) / (Общие оценки)
Почему это неправильно : средняя оценка работает нормально, если у вас всегда много оценок, но предположим, что элемент 1 имеет 2 положительных и 0 отрицательных оценок. Допустим, у пункта 2 100 положительных оценок и 1 отрицательная. Этот алгоритм помещает элемент два (тонны положительных оценок) ниже элемента 1 (очень мало положительных оценок). НЕПРАВИЛЬНО.
Сайты, которые совершают эту ошибку : Amazon.com
ПРАВИЛЬНОЕ РЕШЕНИЕ : Оценка = Нижняя граница доверительного интервала оценки Вильсона для параметра Бернулли
Что скажите : нам нужно сбалансировать долю положительных оценок с неопределенностью небольшого числа наблюдений. К счастью, математика для этого была разработана в 1927 году Эдвином Б. Уилсоном. Мы хотим спросить: учитывая мои оценки, существует 95% -ная вероятность того, что «реальная» доля положительных оценок равна по крайней мере какой? Уилсон дает ответ. Принимая во внимание только положительные и отрицательные оценки (т. Е. Не пятизвездочную шкалу), нижняя граница доли положительных оценок определяется следующим образом:
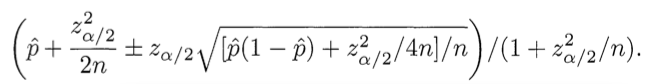
(Используйте минус там, где написано плюс / минус, чтобы вычислить нижнюю границу.) Здесь p̂ – наблюдаемая доля положительных оценок, z α / 2 – квантиль (1-α / 2) стандартного нормального распределения, а n – общее количество оценок. Та же формула реализована в Ruby:
require 'statistics2'
def ci_lower_bound(pos, n, confidence)
if n == 0
return 0
end
z = Statistics2.pnormaldist(1-(1-confidence)/2)
phat = 1.0*pos/n
(phat + z*z/(2*n) - z * Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n)
end
pos– это количество положительных оценок, n– это общее количество оценок, и confidenceотносится к уровню статистической достоверности: выберите 0,95, чтобы иметь 95% вероятность того, что ваша нижняя граница верна, 0,975, чтобы иметь вероятность 97,5% и т. д. z- оценка в этой функции никогда не меняется, поэтому, если у вас нет под рукой статистического пакета или если производительность является проблемой, вы всегда можете жестко запрограммировать здесь значение z. (Используйте 1,96 для уровня достоверности 0,95.)
ОБНОВЛЕНИЕ, апрель 2012 г .: Вот наглядное выражение SQL, которое поможет, если у вас есть widgetsтаблица с положительными и отрицательными рейтингами, и вы хотите отсортировать их по нижней границе 95% доверительного интервала:
SELECT widget_id, ((positive + 1.9208) / (positive + negative) -
1.96 * SQRT((positive * negative) / (positive + negative) + 0.9604) /
(positive + negative)) / (1 + 3.8416 / (positive + negative))
AS ci_lower_bound FROM widgets WHERE positive + negative > 0
ORDER BY ci_lower_bound DESC;
Если ваш начальник не верит, что такой сложный оператор SQL может вернуть полезный результат, просто сравните результаты с двумя другими методами, описанными выше:
SELECT widget_id, (positive - negative)
AS net_positive_ratings FROM widgets ORDER BY net_positive_ratings DESC;
SELECT widget_id, positive / (positive + negative)
AS average_rating FROM widgets ORDER BY average_rating DESC;
Вы быстро увидите, что дополнительная математика заставляет все хорошие вещи всплывать наверх. (Но перед тем, как запускать этот SQL в массивной базе данных, поговорите со своим дружелюбным администратором базы данных о правильном использовании индексов.)
ОБНОВЛЕНИЕ, март 2016: вот та же формула в Excel:
=IFERROR((([@[Up Votes]] + 1.9208) / ([@[Up Votes]] + [@[Down Votes]]) - 1.96 *
SQRT(([@[Up Votes]] * [@[Down Votes]]) / ([@[Up Votes]] + [@[Down Votes]]) + 0.9604) /
([@[Up Votes]] + [@[Down Votes]])) / (1 + 3.8416 / ([@[Up Votes]] + [@[Down Votes]])),0)
Первоначально я разработал этот метод для генератора фактов в стиле Чака Норриса в честь одного из моих профессоров, но с тех пор он стал популярным в таких местах, как Reddit , Yelp и Digg .
ДРУГИЕ ПРИМЕНЕНИЯ
Конечно, доверительный интервал оценки Вильсона предназначен не только для сортировки. Это полезно, когда вы хотите с уверенностью узнать, какой процент людей предпринял какие-либо действия. Например, его можно использовать для:
- Обнаружение спама / злоупотреблений: какой процент людей, увидев этот элемент, отметит его как спам?
- Составьте список «лучших из». Какой процент людей, увидевших этот элемент, отметит его как «лучшее из»?
- Создайте список «Самые рассылаемые по электронной почте»: какой процент людей, видящих эту страницу, нажмет «Электронная почта»?
В самом деле, в списке «с самым высоким рейтингом» может быть более полезным отображать элементы с наибольшим количеством положительных оценок за просмотр страницы, загрузку или покупку , а не положительные оценки за оценку. Многие люди, находящие что-то посредственное, вообще не утруждают себя оценкой; акт просмотра или покупки чего-либо и отказ от оценки содержит полезную информацию о качестве этого элемента.
ИЗМЕНЕНИЯ
- 20 апреля 2016: Добавлена реализация Excel (спасибо Алессандро Аполлони)
- 4 апреля 2012 г .: новая реализация SQL
- 13 ноября 2011 г .: исправлен язык статистической достоверности и соответственно изменен пример кода.
- 15 февраля: Уточнен пример статистической мощности.
- 13 февраля II: «Другие приложения»
- 13 февраля: общие пояснения и ссылка на соответствующую статью в Википедии.
- 12 февраля 2009 г .: Пример из «Неправильного решения №1» был ошибочным. Это было исправлено.
ССЫЛКИ
Доверительный интервал биномиальной пропорции (Википедия)
Агрести, Алан и Брент А. Коул (1998), «Приблизительное лучше, чем« точное »для интервальной оценки биномиальных пропорций», The American Statistician , 52, 119–126.
Уилсон, Е.Б. (1927), «Вероятный вывод, закон преемственности и статистический вывод», Журнал Американской статистической ассоциации , 22, 209–212.
Вы читаете evanmiller.org , случайную подборку математических, технических и размышлений. Если вам это понравилось, вам также могут понравиться:
- Оцените горячность с помощью закона охлаждения Ньютона
- Как читать немаркированный график продаж
- Байесовские средние рейтинги
- Ранжирование элементов с помощью звездного рейтинга: приблизительный байесовский подход
Получайте новые статьи по мере их публикации через Twitter или RSS .
Хотите найти статистические шаблоны в своей базе данных MySQL, PostgreSQL или SQLite? Моя программа статистики рабочего стола Wizard может помочь вам анализировать больше данных за меньшее время и сообщать открытия визуально, не тратя дни на борьбу с бессмысленным синтаксисом команд. Проверить это!

