Les ponts de Königsberg Philip J. Erdelsky 9 juin 2015

Veuillez envoyer vos commentaires, corrections et ajouts par e-mail au webmestre à pje@efgh.com .

original article:http://www.efgh.com/math/koenigsberg.htm

L’un des problèmes classiques en mathématiques est celui des ponts de Königsberg, qui a été résolu par le mathématicien suisse Leonhard Euler au XVIIIe siècle. Il est facile à énoncer et assez facile à résoudre.

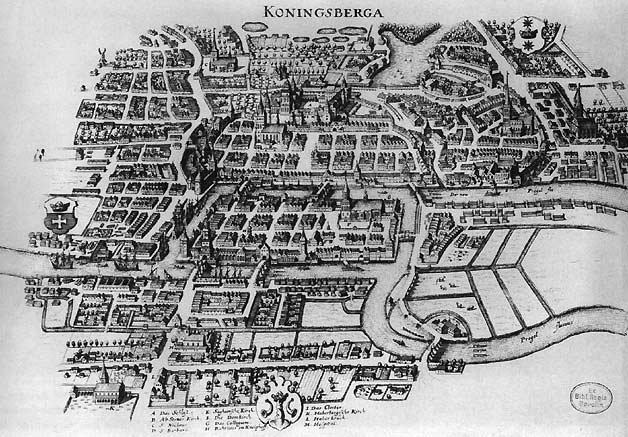
Une rivière traverse la ville de Königsberg (aujourd’hui Kalingrad). Dans la rivière se trouvent deux îles. Sept ponts reliaient les îles et les rives, comme le montre cette ancienne carte:

Les deux canaux fluviaux se rejoignent quelque part sur le côté droit de la carte.

Beaucoup de gens ont essayé de marcher autour de Königsberg, traversant chaque pont une et une seule fois, mais personne ne pouvait le faire. Euler a montré que la tâche est impossible. Sa preuve ne nécessite que quelques connaissances de base en arithmétique et les propriétés des nombres pairs et impairs.

La brillante perspicacité d’Euler, si vous pouvez l’appeler ainsi, était de compter le nombre d’extrémités de pont connectées à chaque lopin de terre:

• 3 sur la rive nord
• 3 sur la rive sud
• 5 sur l’île au centre de la carte
• 3 sur l’île à droite de la carte

Une promenade qui traverse chaque pont une et une seule fois s’appelle, assez convenablement, une promenade d’Euler (ou un chemin d’Euler).

Si une marche d’Euler ne commence ou ne se termine pas sur un terrain particulier, alors il doit y avoir un NOMBRE PAIR de ponts qui y sont connectés, car un marcheur d’Euler qui entre dans la zone par un pont doit en sortir par un autre. Si une marche d’Euler commence ou se termine sur un terrain particulier, le nombre de ponts qui y sont connectés doit être IMPAIR.

Étant donné que chacun des quatre lopins de terre a un nombre impair de ponts qui lui sont reliés, il est évident qu’une promenade d’Euler est impossible.

Les ponts de Königsberg sont un exemple d’une structure mathématique générale appelée graphe .

Un graphe se compose d’un nombre fini de sommets (également appelés nœuds), correspondant aux parcelles de terrain des Ponts de Königsberg, et d’un nombre fini d’arêtes (également appelées lignes), correspondant aux ponts. Nous continuerons de les appeler des ponts. Aussi, pour éviter des difficultés avec des marches inexistantes, nous exigeons qu’il y ait au moins un sommet.

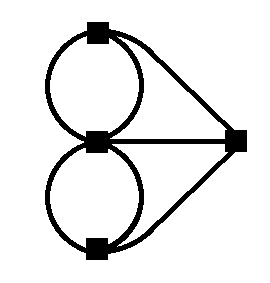
Voici une représentation plus abstraite du graphe de Königsberg:

Un graphique peut être plus général que les ponts de Königsberg. Par exemple, un pont peut connecter un sommet à lui-même, et les sommets n’ont pas besoin d’être confinés à un seul plan. Un sommet isolé, sans ponts de connexion, est également possible.

Le nombre de ponts reliant un sommet particulier est appelé son degré (ou valence).

Les arguments d’Euler ont montré qu’une marche d’Euler n’est possible que si (1) tous les sommets sont de degré pair, auquel cas la marche commence et se termine au même sommet, ou (2) deux sommets, où la marche commence et se termine, sont de degré impair et tous les autres sommets sont de degré pair.

Deux propriétés des promenades d’Euler sont évidentes. L’inverse d’une marche d’Euler est une marche d’Euler, et si une marche d’Euler commence et se termine au même sommet, elle peut également être commencée et terminée à n’importe quel autre sommet.

Ces conditions sont-elles également suffisantes? Évidemment pas. Le graphe doit également être connecté, c’est-à-dire qu’il doit y avoir un chemin (pas nécessairement un chemin d’Euler) de chaque sommet à chaque autre sommet.

Prouver l’existence d’une marche d’Euler pour un graphe connecté sans sommets de degré impair ou deux sommets de degré impair est un peu plus difficile, mais cela n’implique pas de mathématiques avancées.

Tout d’abord, considérons un graphe connexe où tous les sommets sont de degré pair. Commencez à marcher à un sommet, en gardant une trace des ponts que vous avez traversés. Chaque fois que vous entrez dans un sommet, laissez-le par un pont que vous n’avez pas traversé auparavant. Si ce n’est pas le sommet de départ, alors si vous êtes entré par un pont non croisé, vous pouvez toujours le quitter par un autre. Et après votre départ, le sommet a toujours un nombre pair de ponts non croisés.

La marche doit prendre fin lorsque vous revenez au sommet de départ et que vous ne trouvez pas de pont non croisé pour le quitter.

Si vous avez réussi à traverser tous les ponts, la promenade est terminée.

S’il reste au moins un pont non croisé, la marche doit être augmentée.

Notez, cependant, que chaque sommet a toujours un nombre pair de ponts non croisés.

Puisque le graphe est connecté, il y a un chemin entre le sommet de départ et un sommet avec un pont non croisé. Considérez le premier sommet de ce chemin avec un pont non croisé. Ça doit être dans la marche. Appelez-le sommet A.

Commencez maintenant au sommet A et faites une deuxième marche en ne traversant que les ponts que vous n’avez pas encore franchis, que ce soit dans cette marche ou dans la première. Comme précédemment, la marche ne se termine que lorsque vous revenez au sommet A.

Maintenant, combinez les deux promenades en une seule marche. La manière la plus simple de procéder est de commencer la première marche au sommet A. Lorsque vous revenez au sommet A, faites la deuxième marche.

S’il reste au moins un pont non croisé, vous pouvez continuer ce processus jusqu’à ce que tous les ponts aient été traversés.

Vous pouvez vous demander ce qui se passe si le graphe n’a qu’un seul sommet et au moins un pont. Il est facile de montrer que le graphe est connecté, que le sommet a un degré pair et qu’il y a une marche d’Euler. Un graphe avec un seul sommet et aucun pont n’est pas nécessairement une exception, bien que les concepts de connexité et de marche d’Euler soient quelque peu vides dans ce cas.

C’est le résultat souhaité pour un graphe connexe dans lequel chaque sommet est de degré pair. Considérons maintenant un graphe avec deux sommets B et C de degré impair. Créez un graphe légèrement plus grand en insérant un pont reliant les sommets B et C. Tous les sommets de ce graphe sont de degré pair, il a donc une marche d’Euler. Une partie de cette promenade consiste à traverser le nouveau pont du sommet B au sommet C, ou vice-versa.

Il est clair que cette marche d’Euler, sans le nouveau croisement entre les sommets B et C, est une marche d’Euler sur le graphe d’origine.